The traditional approach for determining the fatigue limit for a structure is to establish the S - N curves (load versus number of cycles to failure) for the materials in the structure. Such an approach is still used as a design tool in many cases to predict fatigue resistance of engineering structures. However, this technique is generally conservative, and it does not define a relationship between the cycle number and the degree of damage or crack length.
One alternative approach is to predict the fatigue life by using a crack/damage evolution law based on the inelastic strain/energy when the structure's response is stabilized after many cycles. Because the computational cost to simulate the slow progressive damage in a material over many load cycles is prohibitively expensive for all but the simplest models, numerical fatigue life studies usually involve modeling the response of the structure subjected to a small fraction of the actual loading history. This response is then extrapolated over many load cycles using empirical formulae such as the Coffin-Manson relationship (see Coffin, 1954, and Manson, 1953) to predict the likelihood of crack initiation and propagation. Since this approach is based on a constant crack/damage growth rate, it may not realistically predict the evolution of the crack or damage.
The direct cyclic analysis capability in Abaqus/Standard provides a computationally effective modeling technique to obtain the stabilized response of a structure subjected to periodic loading and is ideally suited to perform low-cycle fatigue calculations on a large structure. The capability uses a combination of Fourier series and time integration of the nonlinear material behavior to obtain the stabilized response of the structure directly. The theory and algorithm to obtain a stabilized response using the direct cyclic approach are described in detail in Direct cyclic algorithm.
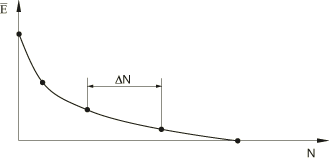
The direct cyclic low-cycle fatigue procedure models the progressive damage and failure both in bulk materials (such as in solder joints in an electronic chip packaging or intra-laminar crack growth in laminated composites) and at material interfaces (such as delamination in laminated composites). The former can be based on either a continuum damage mechanics approach or the principles of linear elastic fracture mechanics with the extended finite element method. The response is obtained by evaluating the behavior of the structure at discrete points along the loading history (see Figure 1). The solution at each of these points is used to predict the degradation and evolution of material properties that will take place during the next increment, which spans a number of load cycles, Δ N . The degraded material properties are then used to compute the solution at the next increment in the load history. Therefore, the crack/damage growth rate is updated continually throughout the analysis.

Figure 1. Elastic stiffness degradation as a function of the cycle number.
The elastic material stiffness at a material point remains constant and contact conditions remain unchanged when the stabilized solution is computed at a given point in the loading history. Each of the solutions along the loading history represents the stabilized response of the structure subjected to the applied period loads, with a level of material damage at each point in the structure computed from the previous solution. This process is repeated up to a point in the loading history at which a fatigue life assessment can be made.
In bulk material, there are two approaches to modeling the progressive damage and failure. One approach is based on continuum damage mechanics. This approach is more appropriate for ductile material, in which the cyclic loading leads to stress reversals and the accumulation of plastic strains, which in turn cause the initiation and propagation of cracks. The damage initiation and evolution are characterized by the stabilized accumulated inelastic hysteresis strain energy per cycle as illustrated in Figure 2. The other approach is based on the principles of linear elastic fracture mechanics with the extended finite element method. This approach is more appropriate for brittle material or material with small scale yielding, in which the cyclic loading leads to material strength degradation causing fatigue crack growth along an arbitrary path. The onset and growth of the crack are characterized by the relative fracture energy release rate at the crack tip based on the Paris law (Paris, 1961).
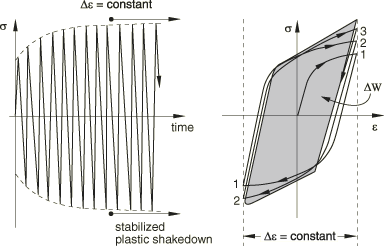
Figure 2. Plastic shakedown in a direct cyclic analysis.
At interfaces of laminated composites the cyclic loading leads to interface strength degradation causing fatigue delamination growth. The onset and growth of delamination are also characterized by the relative fracture energy release rate at the crack tip based on the Paris law (Paris, 1961).
Both the progressive damage mechanism in the bulk material and the progressive delamination growth mechanism at interfaces can be considered simultaneously, with the failure occurring first at the weakest link in a model.
Defining a low-cycle fatigue analysis using the direct cyclic approach is similar to defining a direct cyclic analysis. See Direct cyclic analysis for details on how to specify the number of Fourier terms, number of iterations, and the increment sizes. You specify the maximum numbers of cycles, N m a x , when you define the low-cycle fatigue analysis step.
Input File Usage
DIRECT CYCLIC, FATIGUE first data line , ,
Step module: Create Step: General: Direct cyclic; Fatigue: Include low-cycle fatigue analysis, Maximum number of cycles: Value:
A low-cycle fatigue step using the direct cyclic approach can be the only step in an analysis, can follow a general or linear perturbation step, or can be followed by a general or linear perturbation step. Multiple low-cycle fatigue analysis steps can be included in a single analysis. In such a case the Fourier series coefficients obtained in the previous step can be used as starting values in the current step. By default, the Fourier coefficients are reset to zero, thus allowing application of cyclic loading conditions that are very different from those defined in the previous low-cycle fatigue step.
As in a direct cyclic analysis, you can specify that a low-cycle fatigue step in a restart analysis should use the Fourier coefficients from the previous step, thus allowing continuation of an analysis to simulate more loading cycles. In a low-cycle fatigue analysis a restart file is written at the end of the stabilized cycle. Consequently, a restart analysis that is a continuation of a previous low-cycle fatigue analysis will start with a new loading cycle at t = 0 (see Restarting an analysis).
Input File Usage
Use the following option to specify that the current step is a continuation of the previous low-cycle fatigue step using the direct cyclic approach:
DIRECT CYCLIC, FATIGUE, CONTINUE=YES
Use the following option to reset the Fourier series coefficients to zero:
DIRECT CYCLIC, FATIGUE, CONTINUE=NO (default)
Use the following option to specify that the current step is a continuation of the previous low-cycle fatigue step using the direct cyclic approach:
Step module: Create Step: General: Direct cyclic; Basic: Use displacement Fourier coefficients from previous direct cyclic step; Fatigue: Include low-cycle fatigue analysis
Use the following option to reset the Fourier series coefficients to zero:
Step module: Create Step: General: Direct cyclic; Fatigue: Include low-cycle fatigue analysis
![]()
Low-cycle fatigue analysis in Abaqus/Standard allows modeling of progressive damage and failure for ductile materials in any elements whose response is defined in terms of a continuum-based constitutive model (About the material library). This includes cohesive elements modeled using a continuum approach (Modeling of an adhesive layer of finite thickness). The inelastic definition in a material point must be used in conjunction with the linear elastic material model (Linear elastic behavior), the porous elastic material model (Elastic behavior of porous materials), or the hypoelastic material model (Hypoelastic behavior).
After damage initiation the elastic material stiffness is degraded progressively in each cycle (as shown in Figure 1) based on the accumulated stabilized inelastic hysteresis energy. It is impractical and computationally expensive to perform a cycle-by-cycle simulation for a low-cycle fatigue analysis; Instead, to accelerate the low-cycle fatigue analysis, each increment extrapolates the current damaged state in the bulk material forward over many cycles to a new damaged state after the current loading cycle is stabilized.
Damage initiation refers to the beginning of degradation of the response of a material point. In a low-cycle fatigue analysis the damage initiation criterion is characterized by the accumulated inelastic hysteresis energy per cycle, Δ w . Δ w and material constants are used to determine the number of the cycle in which damage is initiated, N 0 . At the end of a stabilized loading cycle, N , Abaqus/Standard checks to see if the damage initiation criterion N > N 0 is satisfied in any material point; material stiffness at a material point will not be degraded unless this criterion is satisfied. The calculations and output associated with damage initiation are discussed in detail in Damage initiation for ductile materials in low-cycle fatigue.
Once the damage initiation criterion is satisfied at a material point, the damage state is calculated and updated based on the inelastic hysteresis energy for the stabilized cycle. Abaqus/Standard assumes that the degradation of the elastic stiffness can be modeled using the scalar damage variable, D . The rate of the damage in a material point per cycle, d D d N , is calculated based on the accumulated inelastic hysteresis energy, the characteristic length associated with an integration point, and material constants. For details, see Damage evolution for ductile materials in low-cycle fatigue.
Typically, a material has completely lost its load carrying capacity when D = 1 . You can remove an element from the mesh if all of the section points at all integration locations of the element have lost their load carrying capability.
If the damage initiation criterion is satisfied in any material point at the end of a stabilized cycle, N , Abaqus/Standard extrapolates the damage variable D N from the current cycle forward to the next increment over a number of cycles, Δ N . The new damage state, D N + Δ N , is given by
D N + Δ N = D N + Δ N L c 3 Δ w c 4 ,where L is the characteristic length associated with an integration point, and c 3 and c 4 are material constants (see Damage evolution for ductile materials in low-cycle fatigue for more information).
You specify the minimum ( Δ N m i n ) and maximum ( Δ N m a x ) number of cycles over which the damage is extrapolated forward in any given increment. The default values are 100 and 1000, respectively.
Input File Usage
DIRECT CYCLIC, FATIGUE first data line ,
Step module: Create Step: General: Direct cyclic; Fatigue: Include low-cycle fatigue analysis, Cycle increment size: Minimum: , Maximum:
![]()
Low-cycle fatigue analysis in Abaqus/Standard allows the modeling of discrete crack growth along an arbitrary path based on the principles of linear elastic fracture mechanics with the extended finite element method. You complete the definition of the crack propagation capability by defining a fracture-based surface behavior and specifying the fracture criterion in enriched elements. The fracture energy release rates at the crack tips in enriched elements are calculated based on the modified virtual crack closure technique ( VCCT ). VCCT uses the principles of linear elastic fracture mechanics. Therefore, VCCT is appropriate for problems in which brittle fatigue crack growth occurs, although nonlinear material deformations can occur somewhere else in the bulk materials. For more information about defining fracture criteria and VCCT in enriched elements, see Modeling discontinuities as an enriched feature using the extended finite element method.
To accelerate the low-cycle fatigue analysis, the damage extrapolation technique is used, which advances the crack by at least one element length after each stabilized cycle.
The onset and growth of fatigue crack at an enriched element are characterized by using the Paris law, which relates the relative fracture energy release rate, Δ G , to crack growth rates. Two criteria must be met to initiate fatigue crack growth: one criterion is based on material constants, Δ G , and the current cycle number, N ; the other criterion is based on the maximum fracture energy release rate, G m a x , which corresponds to the cyclic energy release rate when the structure is loaded up to its maximum value. Once the onset of fatigue crack growth criterion is satisfied at the enriched elements, the crack growth rate, d a d N , is a piecewise function based on material constants and Δ G (the Paris law). The criteria for fatigue crack onset and growth are discussed in detail in Modeling discontinuities as an enriched feature using the extended finite element method.
If the onset of crack growth criterion is satisfied at any crack tip in the enriched element at the end of a stabilized cycle, N , Abaqus/Standard extends the crack length, a N , from the current cycle forward over a number of cycles, Δ N , to a N + Δ N by fracturing at least one enriched element ahead of the crack tips. Given the material constants c 3 and c 4 (as defined in Modeling discontinuities as an enriched feature using the extended finite element method), combined with the known element length and likely propagation direction Δ a N j = a N + Δ N - a N at the enriched elements ahead of the crack tips, the number of cycles necessary to fail each enriched element ahead of the crack tip can be calculated as Δ N j , where j represents the enriched element ahead of the j th crack tip. The analysis is set up to advance the crack by at least one enriched element per increment after the loading cycle is stabilized. The element with the fewest cycles is identified to be fractured, and its Δ N m i n = m i n ( Δ N j ) is represented as the number of cycles to grow the crack equal to its element length, Δ a N m i n = m i n ( Δ a N j ) . The most critical element is completely fractured with a zero constraint and a zero stiffness at the cracked surfaces at the end of the stabilized cycle. As the enriched element is fractured, the load is redistributed, and a new relative fracture energy release rate must be calculated for the enriched elements ahead of the crack tips for the next cycle. This capability allows at least one enriched element ahead of the crack tips to be fractured after each stabilized cycle and precisely accounts for the number of cycles needed to cause fatigue crack growth over that length.
![]()
Low-cycle fatigue analysis in Abaqus/Standard also allows the modeling of progressive delamination growth at the interfaces in laminated composites. The interface along which the delamination (or crack) propagates must be indicated in the model using a fracture criterion definition. The fracture energy release rates at the crack tips in the interface elements are calculated based on the virtual crack closure technique ( VCCT ). VCCT uses the principles of linear elastic fracture mechanics. Therefore, VCCT is appropriate for problems in which brittle fatigue delamination growth occurs along predefined surfaces, although nonlinear material deformations can occur in the bulk materials. For more information about defining fracture criteria and VCCT , see Crack propagation analysis.
To accelerate the low-cycle fatigue analysis, the damage extrapolation technique is used, which releases at least one element length at the crack tip along the interface after each stabilized cycle. When both brittle fatigue delamination at interfaces and ductile damage or discrete crack growth in bulk materials are considered in an analysis, failure occurs first at the weakest link.
The onset and growth of fatigue delamination at a defined crack interface are characterized by using the Paris law, which relates the relative fracture energy release rate, Δ G , to crack growth rates. Two criteria must be met to initiate fatigue delamination growth: one criterion is based on material constants, Δ G , and the current cycle number, N ; the other criterion is based on the maximum fracture energy release rate, G m a x , which corresponds to the cyclic energy release rate when the structure is loaded up to its maximum value. Once the onset of delamination growth criterion is satisfied at the interface, the delamination growth rate, d a d N , is a piecewise function based on material constants and Δ G (the Paris law). The criteria for fatigue delamination onset and growth are discussed in detail in Low-cycle fatigue criterion.
If the onset of delamination growth criterion is satisfied at any crack tip in the interface at the end of a stabilized cycle, N , Abaqus/Standard extends the crack length, a N , from the current cycle forward over a number of cycles, Δ N , to a N + Δ N by releasing at least one element at the interface. Given the material constants c 3 and c 4 (as defined in Low-cycle fatigue criterion), combined with the known node spacing Δ a N j = a N + Δ N - a N at the interface elements at the crack tips, the number of cycles necessary to fail each interface element at the crack tip can be calculated as Δ N j , where j represents the node at the j th crack tip. The analysis is set up to release at least one interface element per increment after the loading cycle is stabilized. The element with the fewest cycles is identified to be released, and its Δ N m i n = m i n ( Δ N j ) is represented as the number of cycles to grow the crack equal to its element length, Δ a N m i n = m i n ( Δ a N j ) . The most critical element is completely released with a zero constraint and a zero stiffness at the end of the stabilized cycle. As the interface element is released, the load is redistributed, and a new relative fracture energy release rate must be calculated for the interface elements at the crack tips for the next cycle. This capability allows at least one interface element at the crack tips to be released after each stabilized cycle and precisely accounts for the number of cycles needed to cause fatigue crack growth over that length.
![]()
Low-cycle fatigue analysis utilizes the direct cyclic approach to obtain the stabilized cyclic solution iteratively by combining a Fourier series approximation with time integration of the nonlinear material behavior using a modified Newton method. The accuracy of the algorithm depends on the number of Fourier terms used, the number of iterations taken to obtain the stabilized solution, and the number of time points within the load period at which the material response and residual vector are evaluated. Some methods for controlling the solution accuracy in a direct cyclic analysis are described in detail in Direct cyclic analysis. They all remain valid in a low-cycle fatigue analysis using the direct cyclic approach. In addition, the accuracy of a low-cycle fatigue analysis depends on the number of cycles over which the damage is extrapolated forward, as described below.
To accelerate the low-cycle fatigue analysis, the damage extrapolation technique is used at the end of a stabilized cycle. In addition to specifying the minimum and maximum number of cycles over which the damage is extrapolated (see Damage extrapolation technique in the bulk material above), you can specify the damage extrapolation tolerance, Δ D t o l , to control the accuracy of damage extrapolation in the bulk material. The default is Δ D t o l = 1.0 .
Input File Usage
Use the following option to specify the damage extrapolation tolerance:
DIRECT CYCLIC, FATIGUE first data line , , ,
Step module: Create Step: General: Direct cyclic; Fatigue: Include low-cycle fatigue analysis, Damage extrapolation tolerance:
Abaqus/Standard uses an adaptive algorithm to determine the number of cycles over which the damage is extrapolated forward in each increment. By default, Abaqus/Standard starts with 500 cycles (half of the default value of maximum increment in number of cycles) and determines the maximum damage increment at any material points based on
Δ D = Δ N c 3 Δ w c 4 L < Δ D t o l .If the maximum damage increment, Δ D , is greater than the damage extrapolation tolerance that you specify, the number of cycles over which the damage is extrapolated forward is reduced accordingly to ensure the maximum damage increment is less than the damage extrapolation tolerance. On the other hand, if the maximum damage increment at all material points is less than half of the damage extrapolation tolerance that you specify, the number of cycles is increased accordingly to ensure the maximum damage increment is equal to the damage extrapolation tolerance.
To accelerate the low-cycle fatigue analysis and to provide a smooth solution for the crack front, you can specify a nonzero tolerance, Δ D N t o l , for the least number of cycles to fracture an interface element or an enriched element:
L o g Δ N j - L o g Δ N m i n L o g Δ N m i n ≤ Δ D N t o l .
In addition to the interface element or the enriched element that takes the fewest cycles, Δ N m i n , to be fractured, all the other interface or enriched elements that are satisfied by the above condition will be fractured completely.
Input File Usage
Use the following option to specify the tolerance for the least number of cycles to fracture an element:
DIRECT CYCLIC, FATIGUE first data line , , , ,
Specifying a tolerance for the least number of cycles to fracture an element is not supported in Abaqus/CAE .
![]()
Initial values of stresses, temperatures, field variables, solution-dependent state variables, etc. can be specified (see Initial conditions in Abaqus/Standard and Abaqus/Explicit).
![]()
Boundary conditions can be applied to any of the displacement or rotation degrees of freedom. During the analysis, prescribed boundary conditions must have an amplitude definition that is cyclic over the step: the start value must be equal to the end value (see Amplitude Curves). If the analysis consists of several steps, the usual rules apply (see Boundary conditions in Abaqus/Standard and Abaqus/Explicit). At each new step the boundary condition can either be modified or completely defined. All boundary conditions defined in previous steps remain unchanged unless they are redefined.
![]()
The following loads can be prescribed in a low-cycle fatigue analysis using the direct cyclic approach:
During the analysis each load must have an amplitude definition that is cyclic over the step where the start value must be equal to the end value (see Amplitude Curves). If the analysis consists of several steps, the usual rules apply (see About loads). At each new step the loading can either be modified or completely defined. All loads defined in previous steps remain unchanged unless they are redefined.
![]()
The following predefined fields can be specified in a low-cycle fatigue analysis using the direct cyclic approach, as described in Predefined Fields:
![]()
Most ductile material models that describe mechanical behavior are available for use in a low-cycle fatigue analysis. The inelastic definition in a material point must be used in conjunction with the linear elastic material model (Linear elastic behavior), the porous elastic material model (Elastic behavior of porous materials), or the hypoelastic material model (Hypoelastic behavior).
The following material properties are not active during a low-cycle fatigue analysis: acoustic properties, thermal properties (except for thermal expansion), mass diffusion properties, electrical conductivity properties, piezoeletric properties, and pore fluid flow properties.
Rate-dependent yield (Rate-dependent yield), rate-dependent creep (Rate-dependent plasticity: creep and swelling), and two-layer viscoplasticity (Two-layer viscoplasticity) can also be used during a low-cycle fatigue analysis.
![]()
Any of the stress/displacement elements in Abaqus/Standard can be used in a low-cycle fatigue analysis (see Choosing the appropriate element for an analysis type). This includes cohesive elements with finite thickness (Modeling of an adhesive layer of finite thickness). However, when modeling fatigue crack growth based on the principles of linear elastic fracture mechanics with the extended finite element method, only first-order continuum stress/displacement elements and second-order stress/displacement tetrahedron elements can be associated with an enriched feature (see Modeling discontinuities as an enriched feature using the extended finite element method).
![]()
Different types of output are available for postprocessing and for monitoring a low-cycle fatigue analysis using the direct cyclic approach.
As in a direct cyclic analysis, low-cycle fatigue analysis using the direct cyclic approach in Abaqus/Standard prints the residual force, time average force, and a flag to indicate if equilibrium was satisfied in the message ( .msg ) file at different time increments for each iteration in each loading cycle. You can control the frequency in increments at which information is printed to the message file, and you can suppress the output; the default is to print output every 10 increments (see The Abaqus/Standard message file for more information).
Abaqus/Standard also prints the number of Fourier terms used, the maximum residual coefficient, the maximum correction to displacement coefficients, and the maximum displacement coefficient in the Fourier series in the message file at the end of each iteration in each cycle. An example of the output is shown below:
CYCLE 5 STARTS ITERATION 26 STARTS INC TIME STEP LARG. RESI. TIME AVG. FORCE INC TIME FORCE FORCE EQUV. 10 0.250 2.50 1.008E+01 50.9 N 20 0.250 5.00 1.622E+01 76.8 N 30 0.250 7.50 4.622E-02 99.8 Y ITERATION 26 SUMMARY NUMBER OF FOURIER TERMS USED 40, TOTAL NUMBER OF INCREMENTS 120 CYCLE/STEP TIME 30.0, TOTAL TIME COMPLETED 31.0 AVERAGE FORCE 21.2 TIME AVG. FORCE 25.7 MAX. COEFFICIENT OF DISP. 0.142 AT NODE 24 DOF 2 MAX. COEFF. OF RESI. FORCE ON CONST. TERM 31.7 AT NODE 44 DOF 1 MAX. COEFF. OF RESI. FORCE ON PERI. TERMS 0.82 AT NODE 6 DOF 3 MAX. CORR. TO COEFF. OF DISP. ON CONST. TERM 0.002 AT NODE 50 DOF 3 MAX. CORR. TO COEFF. OF DISP. ON PERI. TERMS 0.015 AT NODE 50 DOF 3
Element and nodal output are written only when the stabilized cycle is reached. If a stabilized cycle has not been reached at the end of a cycle, output is written for the last iteration of the cycle. All standard output variables in Abaqus/Standard (Abaqus/Standard output variable identifiers) are available. In addition, the following variables are available for progressive damage in bulk ductile material based on the continuum damage mechanics approach:
Status of element (the status of an element is 1.0 if the element is active, 0.0 if the element is not).
Scalar stiffness degradation, D .
Number of cycles to initialize the damage at the material point.
The following variables are available for discrete crack propagation along an arbitrary path based on the principles of linear elastic fracture mechanics with the extended finite element method:
Status of the enriched element. (The status of an enriched element is 1.0 if the element is completely cracked, 0.0 if the element is not. If the element is partially cracked, the value lies between 1.0 and 0.0.)
Number of cycles to initialize the crack at the enriched element.
All components of strain energy release rate range; i.e., the difference between the energy release rate at the maximum loading and at the minimum loading.
You may want to recover additional results for a stabilized cycle. You can extract these results from the restart data (see Recovering additional results output from restart data in Abaqus/Standard).
Input File Usage
POST OUTPUT, CYCLE=n
Recovering additional results for a stabilized cycle is not supported in Abaqus/CAE .
Output at exact times is not supported for low-cycle fatigue analysis. If output at exact times is requested, Abaqus will issue a warning message and change the output to an output at approximate times.
![]()
A low-cycle fatigue analysis using the direct cyclic approach is subject to the following limitations:
![]()
The following is an example of modeling progressive damage and failure in the bulk material based on the continuum damage mechanics approach and progressive delamination growth at the interface:
HEADING … BOUNDARY Data lines to specify zero-valued boundary conditions INITIAL CONDITIONS Data lines to specify initial conditions AMPLITUDE Data lines to define amplitude variations ** MATERIAL Options to define material properties DAMAGE INITIATION, CRITERION=HYSTERESIS ENERGY Data lines to define material constants for bulk ductile material damage initiation DAMAGE EVOLUTION, TYPE=HYSTERESIS ENERGY Data lines to define material constants for bulk ductile material damage evolution ** SURFACE, NAME=slave Data lines to define slave surface at delamination interface SURFACE, NAME=master Data lines to define master surface at delamination interface CONTACT PAIR slave, master ** STEP (,INC=) Set INC equal to the maximum number of increments in a single loading cycle DIRECT CYCLIC, FATIGUE Data line to define time increment, cycle time, initial number of Fourier terms, maximum number of Fourier terms, increment in number of Fourier terms, and maximum number of iterations Data line to define minimum increment in number of cycles, maximum increment in number of cycles, total number of cycles, and damage extrapolation tolerance DEBOND, SLAVE=slave, MASTER=master FRACTURE CRITERION, TYPE=FATIGUE Data lines to define material constants used in Paris law and fracture criterion ** BOUNDARY, AMPLITUDE= Data lines to prescribe zero-valued or nonzero boundary conditions CLOAD and/or DLOAD, AMPLITUDE= Data lines to specify loads TEMPERATURE and/or FIELD, AMPLITUDE= Data lines to specify values of predefined fields ** END STEP
The following is an example of modeling discrete crack growth in the bulk material based on the principles of linear elastic fracture mechanics with the extended finite element method and progressive delamination growth at the interface:
HEADING … ENRICHMENT, TYPE=PROPAGATION CRACK, INTERACTION=INTERACTION, ELSET=ENRICHED BOUNDARY Data lines to specify zero-valued boundary conditions INITIAL CONDITIONS Data lines to specify initial conditions AMPLITUDE Data lines to define amplitude variations ** MATERIAL Options to define material properties SURFACE, INTERACTION=INTERACTION SURFACE BEHAVIOR FRACTURE CRITERION, TYPE=FATIGUE Data lines to define material constants used in the Paris law and fracture criterion in the bulk material for enriched elements ** SURFACE, NAME=slave Data lines to define slave surface at delamination interface SURFACE, NAME=master Data lines to define master surface at delamination interface CONTACT PAIR slave, master ** STEP (,INC=) Set INC equal to the maximum number of increments in a single loading cycle DIRECT CYCLIC, FATIGUE Data line to define time increment, cycle time, initial number of Fourier terms, maximum number of Fourier terms, increment in number of Fourier terms, and maximum number of iterations Data line to define minimum increment in number of cycles, maximum increment in number of cycles, total number of cycles, and damage extrapolation tolerance DEBOND, SLAVE=slave, MASTER=master FRACTURE CRITERION, TYPE=FATIGUE Data lines to define material constants used in the Paris law and fracture criterion at the interface ** BOUNDARY, AMPLITUDE= Data lines to prescribe zero-valued or nonzero boundary conditions CLOAD and/or DLOAD, AMPLITUDE= Data lines to specify loads TEMPERATURE and/or FIELD, AMPLITUDE= Data lines to specify values of predefined fields ** END STEP
![]()